NI BLOG
ネイチャーインサイト株式会社の情報発信ブログ
SASに関する技術情報など
SASでIPTW(逆確率重み付け法)を実装
SASでIPTW(逆確率重み付け法)を実装
はじめまして、データアナリティクス部のmorishitaと申します。
今回、傾向スコア分析のIPTW(逆確率重み付け法)について調査する機会がありましたので、備忘録も兼ねてブログに執筆することにいたしました。
本記事では、IPTWの基本的な考え方から、実際の解析手順、SASによる実装例について簡単に整理していきたいと思います。
はじめに
観察研究における因果推論では、介入群と非介入群の背景因子の不均衡が、推定結果にバイアスをもたらす大きな要因となります。
この課題に対処するための代表的なアプローチの一つが傾向スコア分析であり、従来から用いられてきたマッチングや層別化に加え、近年ではIPTW(Inverse Probability of Treatment Weighting)と呼ばれる手法が注目を集めています。
今回はこのIPTWをSASで実装する方法を紹介します。
傾向スコアマッチングとIPTW
傾向スコア分析の手法の一つに、傾向スコアマッチングがあります。
個々の患者が一方の治療を受ける傾向をスコア化した値を傾向スコア(Propensity Score, PS)といいます。傾向スコアは、患者がもつ背景因子によって予測可能です。傾向スコアがほぼ等しい患者同士の背景因子は、全く同一とはいえなくてもほどほどに近いといえます。
そこで、傾向スコアがほぼ等しい患者のペアを順に選ぶことを傾向スコアマッチングといいます。傾向スコアマッチングを行うことにより擬似ランダム化が可能になりますが、マッチングの際にレコード数の減少や、患者背景がどちらかの群に偏る可能性があるなどの問題もあります。
これに対して、逆確率による重み付けをIPTW(inverse probability of treatment weighting)といいます。
逆確率による重み付けは、各患者が治療を受ける確率の逆数を用いて重み付けを行うことにより、治療A群と治療B群間で患者背景のバランスが取れた集団を作成する方法です。
この操作により、処置群、非処置群の全員がどちらの処置も同じ確率で受けたような状態となり、背景因子の分布が一致するように調整された「疑似的な無作為割り付け群」となります。
傾向スコアマッチングでは治療群における平均処置効果(ATT)の推定のみが可能でしたが、IPTWにより、平均処置効果(ATE)の推定が可能になります。
傾向スコアマッチング vs IPTW 比較表
| 項目 | 傾向スコアマッチング | IPTW |
|---|---|---|
| 目的 | 治療群と対照群で交絡因子を均等にする | 全サンプルを使って交絡因子を調整し、疑似ランダム化を目指す |
| 手法の概要 | 傾向スコアが近いペアをマッチング | 傾向スコアの逆数を重みとして使用 |
| 使用データ | 一部のサンプル(マッチできたもの)のみ使用 | 全データを使用 |
| 推論対象 | マッチングされたサンプルの範囲(ATT) | 母集団全体(ATE) |
| アウトカム推定方法 | マッチ後のペアで差を比較 | 重み付け後に回帰モデルなどで効果を推定 |
| 問題点 | マッチできないケースを除外するため、バイアスや外的妥当性に影響 | 極端な重みをとるレコードがある場合、推定が不安定になる |
重み付け係数の計算
ATEでは治療群は傾向スコアの逆数[1/PS]、対照群は1-PSの逆数[1/(1-PS)]により重み付けを行います。
例)
傾向スコア:
0.9
治療群の場合:
1 / 0.9 = 1.11… → 1.11倍
対照群の場合:
1 / (1 – 0.9) = 10.0 → 10.0倍
このような操作によって見かけ上、治療群と対照群の患者数は等しくなり、患者背景も均質化されます。
IPTW後のアウトカム集計のイメージ
| ID | 処置(T) | アウトカム(Y) | 傾向スコア(PS) | IPTW重み | 重み付きY |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 0.2 | 1 / 0.2 = 5.00 | 1 × 5.00 = 5.00 |
| 2 | 1 | 0 | 0.4 | 1 / 0.4 = 2.50 | 0 × 2.50 = 0.00 |
| 3 | 1 | 1 | 0.6 | 1 / 0.6 = 1.67 | 1 × 1.67 = 1.67 |
| 4 | 0 | 0 | 0.2 | 1 / (1 – 0.2) = 1.25 | 0 × 1.25 = 0.00 |
| 5 | 0 | 1 | 0.4 | 1 / (1 – 0.4) = 1.67 | 1 × 1.67 = 1.67 |
| 6 | 0 | 0 | 0.6 | 1 / (1 – 0.6) = 2.50 | 0 × 2.50 = 0.00 |
重み付き平均アウトカム(POM)
治療群(T=1):
治療群の重み付き加重平均は、処置を受けた観測値において、アウトカムを逆確率で重み付けした合計を、逆確立の重みの合計で割ったものとして推定されます
\[加重平均Y_1=\frac{5.00+0.00+1.67}{5.00+2.50+1.67}=\frac{6.67}{9.17}\approx0.728\]
対照群(T=0):
対照群の重み付き加重平均は、処置を受けなかった観測値において、アウトカムを逆確率で重み付けした合計を、逆確立の重みの合計で割ったものとして推定されます
\[加重平均Y_0=\frac{0.00+1.67+0.00}{1.25+1.67+2.50}=\frac{1.67}{5.42}\approx0.308\]
ATE(平均処置効果)
推定された2つの重み付き平均アウトカム (POMs) の差として、ATEが推定されます
\[ATE=加重平均Y_1-加重平均Y_0=0.728-0.308=0.420\]
これは、IPTWによって交絡因子の影響を除いた処置の効果が、平均的に42pt改善したことを表します。
SASによる実装
SASによる因果推論用プロシジャ
| プロシジャ | 推定対象 | 主な用途 | 具体例 |
|---|---|---|---|
| PSMATCH | ATE, ATT, ATU | 傾向スコアの推定とマッチング | 年齢・性別・基礎疾患を用いてマッチング後、治療効果を評価し新薬Aと標準治療Bの治療効果を比較 |
| CAUSALTRT | ATE, ATT, ATU | 傾向スコアを利用した処置効果(ATE,ATT)の推定 | 広告キャンペーンが購入行動に及ぼす影響の平均処置効果(ATE)を評価 |
| CAUSALMED | ATE, NIE, NDE | 処置→媒介変数→結果変数の経路における媒介効果を推定 | ストレスが健康に与える影響が睡眠を媒介しているかどうかを検証 |
| CAUSALGRAPH | 識別分析 | 因果ダイアグラム(DAG)を用いた因果構造の視覚化と解析 | 医療介入に対する交絡因子の視覚的特定と解析プランの設計 |
- NIE (Natural Indirect Effect):独立変数が媒介変数を通じて従属変数に与える間接効果。
- NDE (Natural Direct Effect):独立変数が媒介変数を介さずに従属変数に直接与える効果。
因果推論分析における実践的なフローとしては、CAUSALGRAPHプロシジャで処置、効果、交絡因子、媒介因子の関係を視覚化し、因果構造の定義と仮説設定を行ってから、PSMATCHプロシジャやCAUSALTRTプロシジャで傾向スコアの推定と処置効果の推定を行います。
その後、必要に応じてCAUSALMEDプロシジャで媒介効果の分析を行います。
上記プロシジャの中でIPTWを実装できるのは、PSMATCHプロシジャとCAUSALTRTプロシジャです。ここからはIPTW(逆確率重み付け)の実装方法について紹介していきます。
PSMATCHプロシジャ
傾向スコア分析を行うための、傾向スコアの計算や以前に計算された傾向スコアの読み取り、傾向スコアを用いた重み付けや層別化などの手法を提供します。また、各治療対象レコードを傾向スコアが類似する1つ以上の対照ユニットとマッチングさせます。
PSMATCHプロシジャは傾向スコア分析の「前処理」として、共変量のバランスを改善するためのデータセットの作成に焦点を当てているため、単体ではアウトカム分析を行うことができません。
そのため、PSMATCHプロシジャで傾向スコアを推定後別のプロシジャを用いてアウトカム分析を行う必要があります。
PROC PSMATCH DATA=<データセット名> REGION=ALLOBS;
CLASS <治療変数> <共変量(カテゴリ)>;
PSMODEL <治療変数>(TREATED='1') = <共変量(全て)>;
ASSESS ps var=(<群間差を評価したい変数>) / weight=atewgt ;
OUTPUT OUT(OBS=all)=<出力データセット名> PS=<傾向スコア> atewgt=<重み>;
RUN;
ASSESSステートメントでPSオプションを使用することで、指定した変数の標準化差を表示することができます。
標準化差の絶対値が0.1以下であれば、群間でバランスが取れているといえます。
WEIGHT=ATEWGTを指定することで、逆確率によって重み付けされた変数評価を要求します。
ASSESSステートメントでは数値変数と二値のカテゴリ変数が指定可能です。

標準化差の計算例
連続データの標準化差(SMD)は下記の計算式で求められます。
\[SMD=\frac{\bar{X}_A-\bar{X}_B}{\sqrt{\frac{S^2_A+S^2_B}{2}}}\]
\[\bar{X}_A,\bar{X}_B:A群、B群における平均値\]
\[S^2_A,S^2_B:A群、B群における分散(=標準偏差の二乗)\]
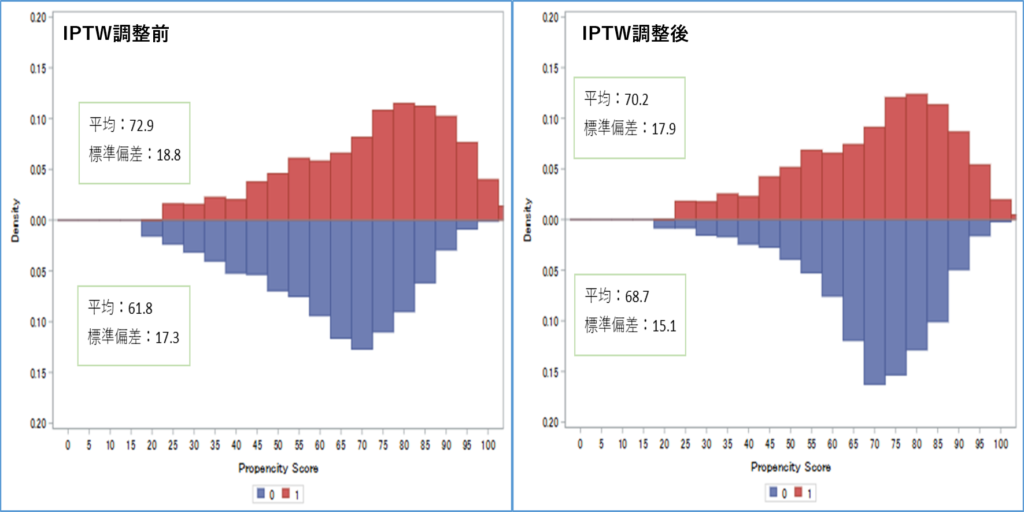
例として、治療群、対照群における年齢の標準化差を計算してみます。
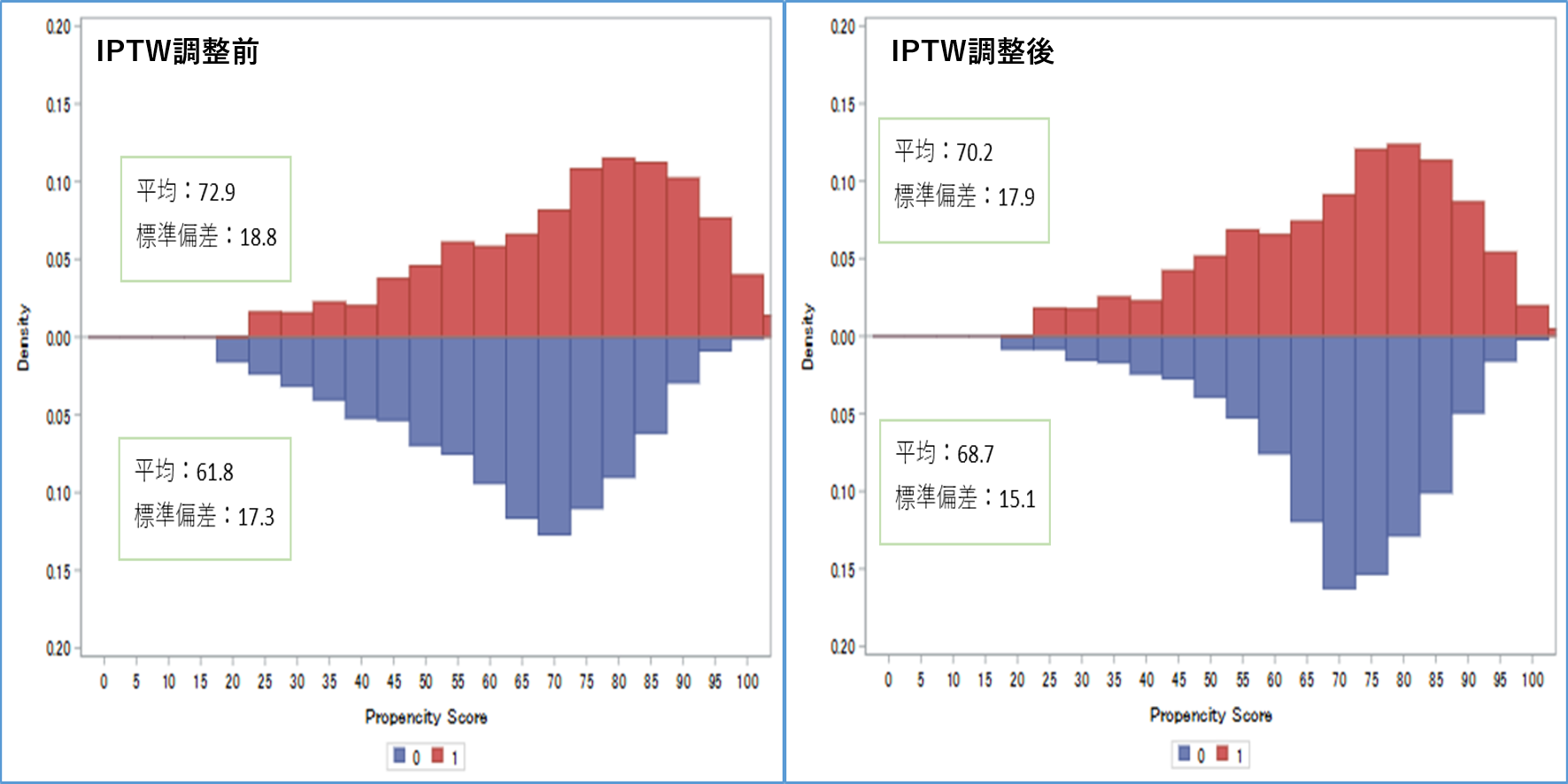
マッチング前の各群の年齢の分布と平均、標準偏差を次の通りとします。

標準化差の計算式に当てはめると
\[SMD=\frac{72.9-61.8}{\sqrt{\frac{18.8^2+17.3^2}{2}}}=\frac{11.1}{18.1}\approx0.6\]
となり、マッチング前の標準化差は約0.6となりました。
次に、PSMATCHプロシジャを用いて傾向スコアマッチングします。
マッチング後の各群の年齢の分布と平均、標準偏差は以下のようになりました。

標準化差の計算式に当てはめると
\[SMD=\frac{70.2-68.7}{\sqrt{\frac{17.9^2+15.1^2}{2}}}=\frac{1.5}{16.6}\approx0.09\]
となり、マッチング後の標準化差は約0.09となりました。
標準化差はマッチング前後で0.6→0.09になり、0.1以下であるのでバランスされているといえます。
治療効果の推定
PSMATCHプロシジャを用いて得られた結果を基に、治療効果の推定を行う必要があります。
評価には、FREQプロシジャとSURVEYLOGISTICプロシジャを使用した例を紹介します。
・FREQプロシジャ
重み付きクロス集計を行うことで、治療効果を推定します。
proc freq data=<入力データセット>;
table <治療変数>*<アウトカム> / chisq or;
weight <重みの変数>;
run;
TABLEステートメントでCHISQオプションを指定することで、カイ二乗検定による治療とアウトカムの統計的な有意差を評価します。また、oddsratio(or)オプションを指定することでオッズ比と信頼区間を出力することができます。
WEIGHTステートメントでPSMATCHで得られた重みの変数を指定することで、重みを考慮した結果を算出できます。
重み付きデータにおけるオッズ比の正確性には限界があるため、より信頼性の高い推定が必要な場合はLOGISTICプロシジャやSURVEYLOGISTICプロシジャを使用するのが一般的です。

・SURVEYLOGISTICプロシジャ
SURVEYLOGISTIC プロシジャは、基本的にロジスティック回帰分析を実行するという点でLOGISTICプロシジャと類似していますが、複雑な標本調査設計を考慮に入れた分析を行うように設計されている点においてLOGISTICプロシジャとは異なります。
IPTWのような重みを考慮したい場合は、SURVEYLOGISTICプロシジャを使用することが統計的に正しい推測を行う上で重要です。
PROC SURVEYLOGISTIC DATA=<入力データセット>;
class <共変量(カテゴリ)> <治療変数>(REF='基準とする値');
MODEL <アウトカム>(EVENT='1') = <共変量> ;
WEIGHT <重みの変数>;
RUN;
CLASSステートメントでREFオプションを指定すると、オッズ比を算出する際の基準とする値を指定することができます。

CAUSALTRTプロシジャ
様々な手法(IPW, REGADJ, Doubly Robust)を用いてATEやATTを推定し、モデルの指定、推定の精度評価、共変量バランスの確認といった分析の各段階をサポートする機能を備えています。
アウトカムが連続型あるいは離散型で、治療変数が二値である場合の平均因果効果の推定が可能です。
PROC CAUSALTRT DATA=<データセット名> METHOD=IPW COVDIFFPS;
CLASS <治療変数> <共変量(カテゴリ)>;
PSMODEL <治療変数>(REF='水準') = <共変量(全て)>;
MODEL <アウトカム> = <共変量>; /* 結果モデル */
OUTPUT OUT=<出力データセット名> PS=<傾向スコア> IPW=<重み>;
RUN;
因果効果の推定結果は以下の表で得られます。
ATE推定値がプラスの値であれば、指定した水準の治療が平均的に効果的であることを示しています。

- POM:潜在的アウトカム平均の推定値
- ATE:ATEの推定値
CAUSALTRTステートメントでCOVDIFFPSオプションを指定することで、傾向スコアモデルの共変量の標準化差を出力することができます。
二値以上のカテゴリ変数に対しても対応しています。

おわりに
今回は、傾向スコア分析の中でも代表的な手法である逆確率重み付け法(IPTW)について、基本的な考え方から実装方法までの概要を整理しました。
因果推論では、解析手法の選択が結果の解釈に大きく影響するため、各手法の前提や適用条件を正しく理解することが重要です。今後も他の手法についても学びを深めていきたいと考えています。
最後までお読みいただきありがとうございました。

















コメント