線形回帰の過学習を抑えよう ～Ridge回帰とLasso回帰～

はじめに

線形回帰は連続変数の予測モデルとして優れたモデルであるが、説明変数が増えると過学習してしまうことがある。
Ridge回帰とLasso回帰は過学習を抑えるために正則化項の概念を入れた線形回帰である。今回はそれについて以下の内容で解説する。

1. 過学習と正則化について

過学習とは

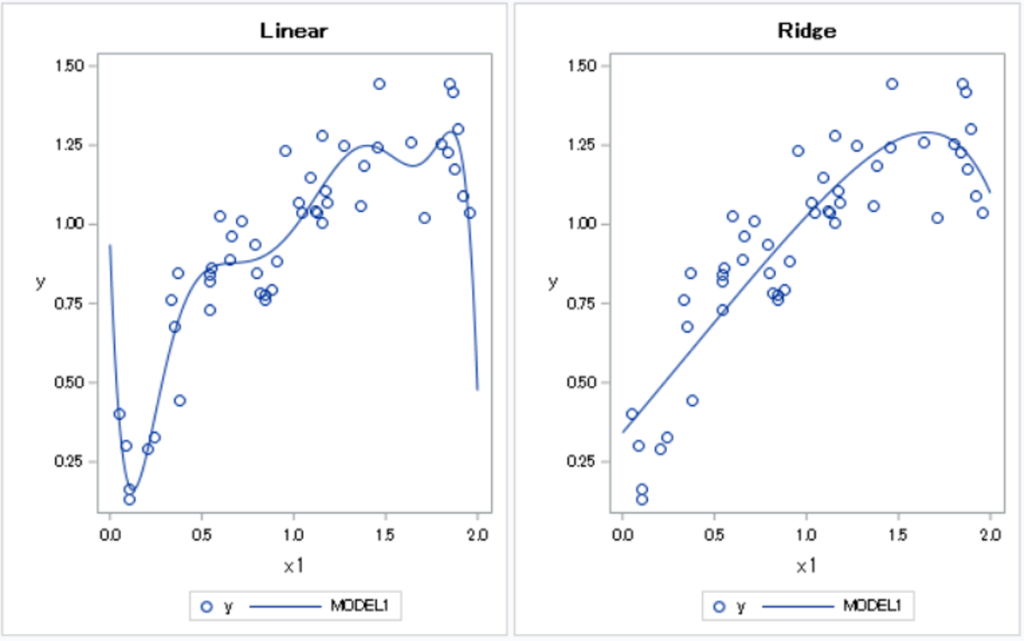
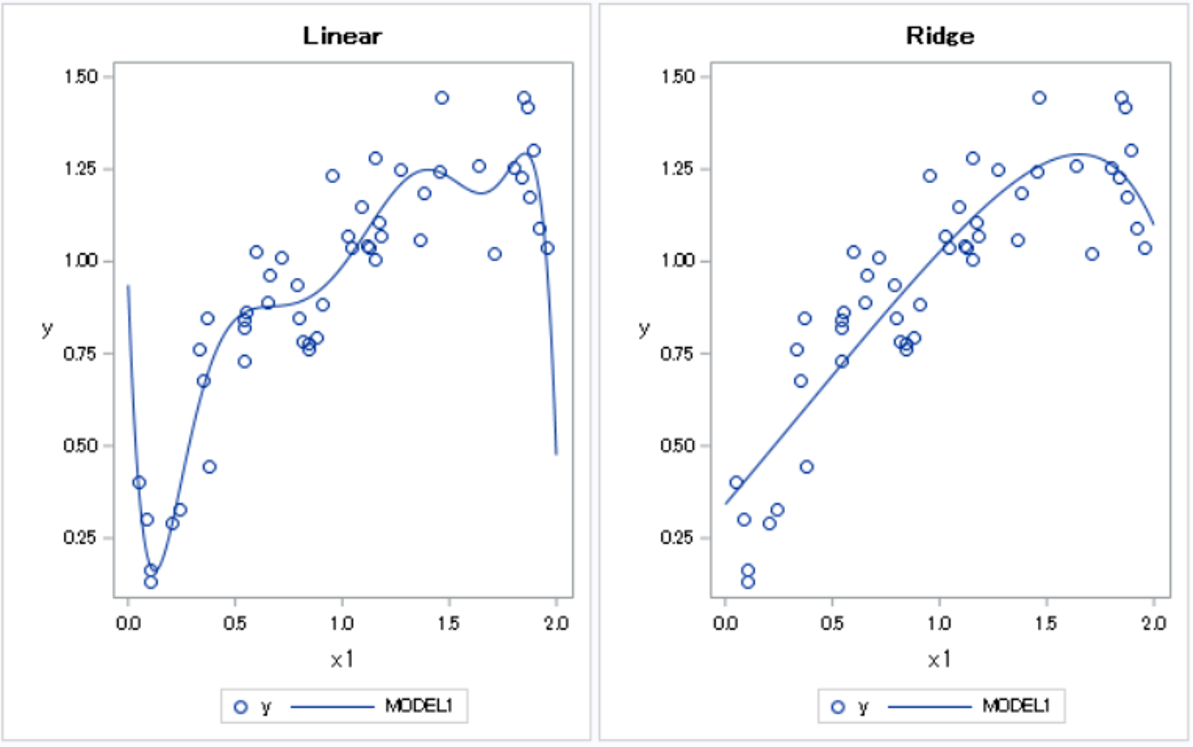
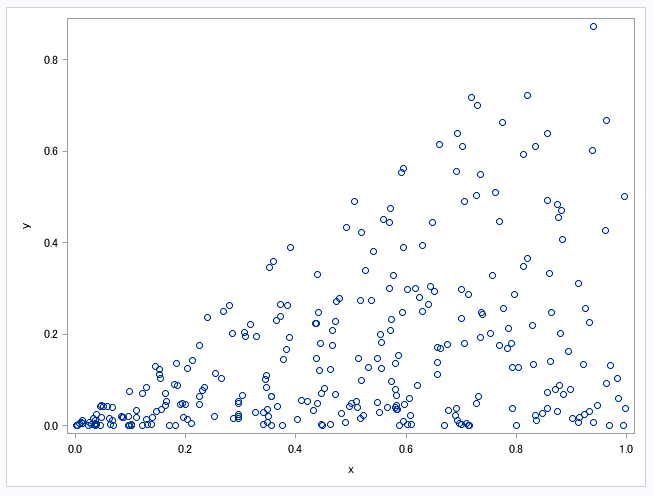
以下のデータに対して\(x,\cdots,x^{10}\)を説明変数として回帰分析を行ってみる(左が線形回帰、右がRidge回帰)。

さて、どちらの曲線がうまく予測できているだろうか?

左側の線形回帰のほうが訓練データに対しての当てはまりはよい。しかし、予測とは未知のデータに対して当てはまりをよくすることである。左の曲線は訓練データを過剰に学習していて、未知のデータへの当てはまりは悪くなっている可能性が高い。このような現象を過学習という。線形回帰では、説明変数を多く投入すると過学習を起こす場合がある。

これを防ぐには、以下のような方法がある。

右側のRidge回帰は線形回帰に正則化項を入れることによって、過学習を防いでいる。

正則化とは

先ほどの線形回帰の標準偏回帰係数を見てみる。

過学習を起こすとそれぞれの標準偏回帰係数の絶対値が非常に大きくなる。傾きが大きいと曲線の波が細かく、大きくなるイメージだ。
これを防ぐために損失関数に標準偏回帰係数の大きさを表す項を入れる。これを正則化項と呼ぶ。

2. Ridge回帰とRasso回帰

損失関数と正則化項

線形回帰の最小2乗法で回帰係数を求めるときの損失関数を示す。(\(\hat{y}\)は予測値)
$$E_{OLS}=\sum_{i=1}^{N}(y_i-\hat{y}_i)^2$$
Ridge回帰、Lasso回帰の損失関数は以下のとおりである。(\(\lambda\)は分析者が決定するパラメータ、\(N\)はデータ数、\(K\)は説明変数の個数。)

$$E_{Ridge}=\sum_{i=1}^{N}(y_i-\hat{y}_i)^2+\frac{1}{2}\lambda\sum_{k=1}^K\beta_k^2$$
$$E_{Lasso}=\sum_{i=1}^{N}(y_i-\hat{y}_i)^2+\lambda\sum_{k=1}^K|\beta_k|$$
線形回帰の損失関数に、Ridge回帰では偏回帰係数の2乗和(L2正則化項)、Lasso回帰では偏回帰係数の絶対値の和(L1正則化項)を追加している。もし偏回帰係数が大きくなった場合、正則化項が大きくなって損失が増えてしまうため、偏回帰係数が大きくなりにくい。したがって、線形回帰よりも過学習しにくい。

下図は偏回帰係数の推定結果である。(上段が線形回帰、下段が\(\lambda=0.02\)のRidge回帰)

線形回帰に比べて偏回帰係数の値が小さくなっており、過学習が抑えられている。

ちなみに、Ridge回帰、Lasso回帰ともに標準化は必須である。

Ridge回帰とLasso回帰の違い

Ridge回帰もLasso回帰も正則化された線形回帰であるが、偏回帰係数の減衰の仕方が異なる。\(\lambda\)と\(\beta\)の関係について結果を見てみよう。(\(x,\cdots,x^5\)を説明変数とした。)

\(\lambda\)が増加するにつれ、Ridge回帰は少しずつ偏回帰係数を小さくしていくが、Lasso回帰は影響度の小さい説明変数の偏回帰係数をちょうど0にすることがわかる。すなわち、Ridge回帰は全体の説明変数を使用しつつ偏回帰係数を小さくするのに対して、Lasso回帰は変数を選択して線形回帰を行っていると解釈できる。

3. SASでの使い方

Ridge回帰

Ridge回帰については、proc regでridgeオプションを使用する。

proc reg data = SASHELP.BASEBALL outest=b ridge=0.001 to 0.02 by 0.001 plots=all;
	model logSalary = CrAtBat--CrBB/STB;
run;
proc print data = b;
run;

結果(一部抜粋)

パラメータ\(\lambda\)が大きくなるにつれ、偏回帰係数が小さくなっている。
注意点として、_RMSE_の値は訓練データに対しての当てはまりなのでこれを基準に選ばないように。

未知のデータtestに対して当てはめたければ、以下を実行しよう。

/*未知のデータ(仮)*/
data test;
	set SASHELP.BASEBALL;
run;
proc reg data = SASHELP.BASEBALL outest=b ridge=0.02;
	model logSalary = CrAtBat--CrBB/STB;
run;
proc score data=test out=test_p score=b type=ridge;
	var CrAtBat--CrBB;
run;

Lasso回帰

Lasso回帰はproc regではできないので、proc glmselectを使用する。

proc glmselect data=SASHELP.Baseball plots=all;
 	model logSalary = CratBat--CrBB/ 
 		selection=lasso (choose=cv stop=none) cvmethod=random(10) STB;
run;

selection=lassoでlasso回帰で変数選択を行う。chooseの部分のcvはクロスバリデーションで、「random(10)」より、10-holdで行う。
結果(一部抜粋)


最終的に2つの変数のみ使用して線形回帰を行っている。
未知のデータtestに対して当てはめたければ、以下のステートメントを追加しよう。

score data = test out = test_p;

まとめ