SASで欠損データ解析をしよう

はじめに

データ分析を行う際、欠損値を含むデータによく遭遇します。
欠損値を含むデータ分析はかなり難しく、誤った結果を起こしやすいです。
実際に、以下の例を御覧ください。

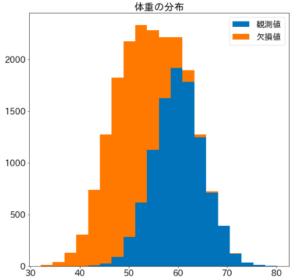
体重データの例

今、欠損値を含む体重のデータがあるとします。
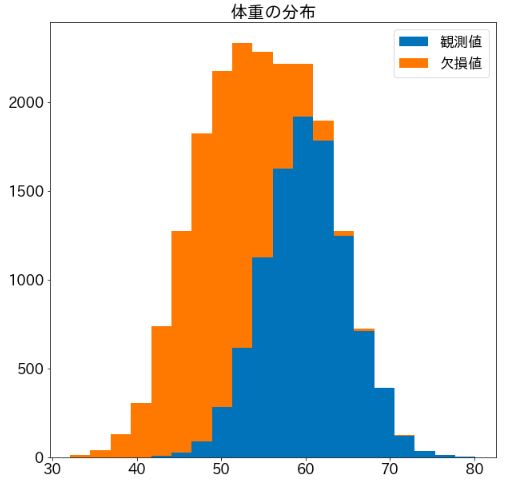
以下は観測できている体重の分布です。

この分布の平均はだいたい60kgでしょうか。
そこで、分析者は「全体の平均の推定値は約60kgだ」と結論付けたとします。

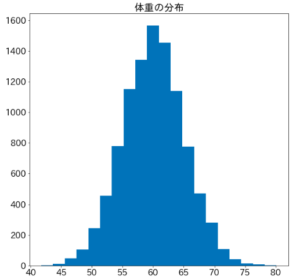
しかし、実は体重の低い人が多く欠損していて、全体の体重は以下の分布でした。

この分布の平均は60kgではありませんね。

このように、何らかのパターンで欠損が起こっているとき、
観測値の平均と実際の平均が大きくずれることがあります。

つまり、欠損値を含むデータから何かを結論付けるとき、
欠損値がどのようなパターンで起こっているのかをしっかり見定める必要があります。

3つの欠損パターン

欠損パターンには、大きく分けて3つあります。
(分かりやすいように書いていますので、正確さに欠けます。
正確に知りたい方は参考文献を読んでください。)

1つ目は、欠損パターンは完全にランダムである場合です。(MCAR)
ランダムのため、欠損のレコードごと削除してしまっても平均値や分散に偏りは生じません。

2つ目は、ある別の変数が欠損パターンに影響している場合です。(MAR)
例えば、身体測定で女性が多く休んだため、女性の体重に欠損が多くなった場合です。
女性の方が全体より軽めであれば、当然体重の平均に偏りが生じることになります。
この場合、例のように観測値だけで平均を出して、それを全体の平均としてしまうと痛い目を見ます。

3つ目は、欠損している変数それ自身が欠損パターンに影響している場合です。(MNAR)
例えば、身体測定で体重が重い人が多く休んだため、重い人の欠損が多い場合です。
こちらも観測できる値のみで平均値を算出すると偏りを生じます。

どれに当てはまるかは、データの値のみから判断するのは難易度が高いです。
実業務では、欠損しているのには何かしらの理由があるはずなので、
その原因の解明や、欠損発生パターンの予想が大切になります。

SASで欠損データ解析

欠損抜きで平均を算出した場合、MARやMNARであると偏りが生じる場合があります。しかし、MARの場合は推定方法によっては偏りのない推定をすることができます。
SASでは、miプロシジャを使用して欠損値の推定をすることができます。
miプロシジャとは多重代入法(multiple imputation)を行い、欠損データ解析を行うプロシジャです。以下の手法が使えます。
・ 線形回帰を繰り返し実施して欠損値を補完するFCSステートメント
・ EMアルゴリズムを使用して尤度関数を最大化するEMステートメント
・ マルコフ連鎖モンテカルロ法による推定を行うMCMCステートメント
etc...

今回は、EMステートメントを用いて平均値を推定してみます。
EMステートメントを使用すると、MCARやMARのときに、欠損しているレコードの他の変数を見ることで、平均、分散共分散を推定することができます。(ただし、(欠損していない値も含めた)変数は多変量正規分布に従うという仮定を置いています。)

実践例

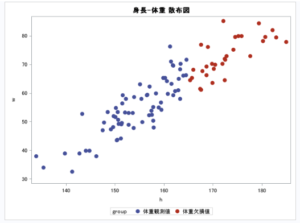
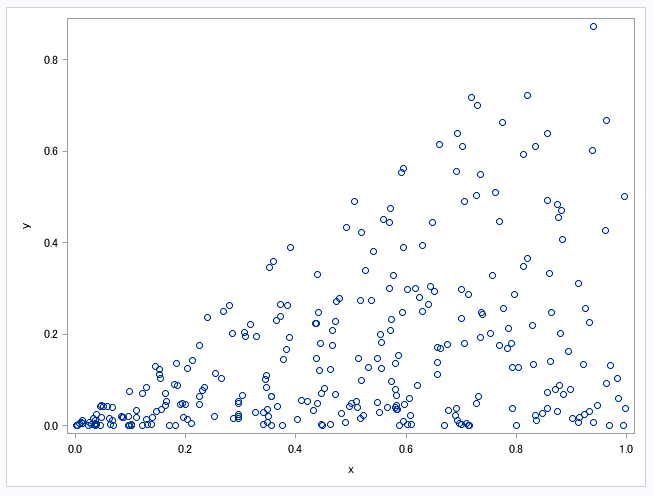
実際に試してみましょう。以下の身長と体重の2変数からなるデータを用意します。

身長が165cm以上の人の体重が欠損値であるとしましょう。

これは身長の値が体重の欠損パターンに影響を及ぼしているのでMARです。

実際にproc meansで平均を計算してみると以下のようになります。

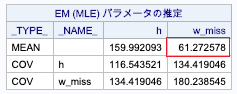
wが全体の体重の平均(60.273kg)、w_missが観測値だけの体重の平均(54.654kg)です。
体重の観測値のみで算出した平均が全体よりかなり小さくなってしまっているのがわかります。

proc miのEMステートメントで推定すると次のようになります。

「w_miss」の「mean」が61.273kgですので、体重の観測値のみで算出した平均よりはかなり偏りが是正されています。

以下が実際のプログラムコードです。

/* データ作成 */

data aaa;

	/*乱数固定*/

	call streaminit(1);

	do i = 1 to 100;

		h = rand("normal",160,10);

		w = h-100+rand("normal",0,5);

		if h>=165 then do;

			w_miss = .;

			group = "体重欠損値";

		end;

		else do;

			w_miss = w;

			group = "体重観測値";	

		end;

		output;

	end;

run;



/* 散布図作成 */

title "身長-体重 散布図";

proc sgplot data=aaa;

	scatter x=h y=w/group = group

	markerattrs=(symbol=CircleFilled size=10);

RUN;



/* そのまま平均値を出すと? */

title "体重の平均値推定(proc means)";

proc means data=aaa;

	var w w_miss;

run;



/* proc miで平均値を予測 */

title "体重の平均値推定(proc mi)";

proc mi data=aaa seed=1 simple nimpute=0;

   em itprint outem=outem;

   var h w_miss;

run;

まとめ

欠損データ解析は非常に難しいです。
また、安易に欠損無視や平均補完等で推定を行うと正しい結果が導かれない可能性があります。
そのため、次の手順で対処を行うことをお勧めします。
1. どのような原因で起こっているのかを解明、予想
2. 欠損パターンの確認
3. 欠損パターンに応じた推定

参考文献

1. M.S. SRIVASTAVA and E.M. CARTER The Maximum Likelihood Method for Non-Response in Sample Surveys
　https://www150.statcan.gc.ca/n1/en/pub/12-001-x/1986001/article/14441-eng.pdf?st=WZ_wawFV
2. 渡辺美智子 山口和範 著 EMアルゴリズムと不完全データの諸問題
3. 欠損値があるデータの分析
　http://norimune.net/1811
4. 欠損値があるデータを扱うＭＩプロシジャについて
　http://www.sas.com/offices/asiapacific/japan/usergroups/wg/archive/001201ono.pdf